Scrapping Hotel url from Tripadvisor

Recently I started working on a web scrapping project. The problem was to find the hotels’ url of tripadvisor for a given city to scrap their reviews. Our review scrapper is working fine once we supply the url for given hotel but the problem was finding url. It involves a human to find the url and I wanted to automate the process. After investigating the tripadvisor home page, I automated the whole process of filling data by selenimum.

;some thing went wrong with my firefox update
(defn go-to-tripadv
  "returns tripadvisors urls for city"
  [city]
  (do
    (set-driver! {:browser :firefox})
    (get-url "https://www.tripadvisor.in")
    (wait-until #(= (title) "TripAdvisor: Read Reviews, Compare Prices & Book"))
    (input-text "#GEO_SCOPED_SEARCH_INPUT" city)
    (click "#GEO_SCOPE_CONTAINER .scopedSearchDisplay li")
    (apply quick-fill-submit
           [{"#mainSearch" "Hotel"}
            {"#SEARCH_BUTTON" click}])
    (wait-until
     #(not= (title) "TripAdvisor: Read Reviews, Compare Prices & Book"))
    (let [home-url (current-url)
          page (page-source)
          rest-url (fetch-all-nav-urls page)]
      (quit)
      (cons home-url rest-url))))

It is working fine but I did not like the browser involvement. I was wondering about request send by browser to tripadvisor to fetch the data and I found firefox pluging Firebug.  After analyzing the request I figured out the request (replace city with required city name) and now the whole process is trivial. You can see the whole code github.

(ns tripadvisorurl.core
  (:require [clj-webdriver.taxi :refer :all]
            [net.cgrand.enlive-html :as ehtml]
            [clj-json.core :as json]))


(defn rest-url-from-page [url page-no]
  (let [[f-el s-el t-el] (clojure.string/split url #"-" 3)
        all-page-no
        (map (fn [x] (str "oa" (* 30 x))) (rest (range page-no)))
        final-url
        (map (fn [x] (str f-el "-" s-el "-" x "-" t-el)) all-page-no)] final-url))


(defn fetch-all-nav-urls
  "fetch all the tripadvisor navigation urls for a city"
  [url]
  (as-> (java.net.URL. url) d
    (ehtml/html-resource d)
    (ehtml/select d [:div.pageNumbers :a])
    (last d)
    (first (:content d))
    (cons url
          (if (nil? d) nil
              (rest-url-from-page url (Integer/valueOf d))))))


(defn go-to-tripadv-api
  "Tripadvisor API for fetching JSON and extract url"
  [city]
  (as-> (str "https://www.tripadvisor.in/TypeAheadJson?query="
             city
             "&action=API&types=geo,theme_park&link_type=hotel&details=false") d
    (java.net.URL. d)
    (ehtml/html-resource d)
    (map (comp first :content first :content) d)
    (first d)
    (json/parse-string d)
    (get d "results")
    (first d)
    (get d "url")
    (str "https://www.tripadvisor.in" d)))

(defn parse-hotel-url
  "returns all the hotels from tripadvisor page"
  [url]
  (as-> (java.net.URL. url) d
    (ehtml/html-resource d)
    (ehtml/select d [:a.property_title])
    (map (juxt (comp first :content) (comp :href :attrs)) d)))

Learning Dependent Types

Finally it’s starting to make sense to me. According to Wikipedia “a dependent type is a type that depends on a value”. Let’s try to break this statement and try to find out the closest corresponding concept in Haskell. In Haskell, we define datatype Maybe as

data Maybe a = Just a | Nothing.

What are the values that can be substituted for a? The values that a can take, are Int, Float, Double or any other data type and we call that Maybe is parametrized over type a. So what is the type of a ? In Haskell, we call it Kind[1]. A kind system is essentially a simply typed lambda calculus “one level up”, endowed with a primitive type, denoted * and called “type”, which is the kind of any data type which does not need any type parameters.

λ> :k Int
Int :: *
λ> :k Float
Float :: *
λ> :k (*)
λ> :k Maybe
Maybe :: * -> *
λ> :k (Maybe Int)
(Maybe Int) :: *

If we change the condition that rather that substituting types (Int, Float, Double, Maybe Int) for a, we can substitute it for values like 3, 4 so hypothetically you can think of type of Just 3 as Maybe 3 and not Maybe Int. The hello world program (List with length) of dependent type follow the same intuition.

*HHDL *Data/Vect> :t Vect
Data.VectType.Vect.Vect : Nat -> Type -> Type
*HHDL *Data/Vect> :doc Vect
Data type Vect : Nat -> Type -> Type
    
    
Constructors:
    Nil : Vect 0 a
        
        
    (::) : (x : a) -> (xs : Vect n a) -> Vect (S n) a

Vector is data type takes a natural number (0, 1, 2 …) and type (Int, Float, Double and many more). We can see that on contrary to Haskell, now values are appearing in types. It has two constructor Nil and Cons (::). Nil is vector of length 0 and polymorphic over a. Cons (::) take an element of type a and vector of length n and gives a vector of length of (n + 1). We have computation at the time of type checking and what makes type-checking dependently-typed programs difficult is the problem of type equality. Since expressions can appear in types, deciding whether two types are equal requires deciding whether program expressions are equal. This is quite difficult, and if the programming language permits an unrestricted general recursion operator then it becomes undecidable. If you confine non-termination and other side-effects to a monad or the like, then type-checking can remain decidable [2]. To put it simply, what would happen if we have a expression like this appears at type level? It will not terminate!

nonterm :: a
nonterm = nonterm

What we can do with dependent types. We can write more precise code and reason about their correctness. Here Tyfun is type level function that takes Boolean value and returns a Type. If the value is False then it returns a function type from Nat to Nat and otherwise a function type which takes two natural numbers (Nat) and returns Bool. The boolornat function takes a boolean value and returns the corresponding value level function.

Tyfun : Bool -> Type
Tyfun False = Nat -> Nat
Tyfun True  = Nat -> Nat -> Bool

boolornat : ( b : Bool ) -> Tyfun b
boolornat False = \e  => e + 1
boolornat True = \x => \y => x == y
*Matrix> boolornat True 3 4
False : Bool
Metavariables: Main.addField
*Matrix> boolornat True 3 3
True : Bool
Metavariables: Main.addField
*Matrix> boolornat False 3
4 : Nat

We can capture the properties of matrix multiplication like multiplying two matrices of size M x N and N x P will give matrix of size M x P.

transposeMat : {a : Type} -> {m : Nat} -> {n : Nat} -> Vect m (Vect n a) -> Vect n (Vect m a)
transposeMat  {n = Z}  _  = [] --[[],[],[],[].... all the inner vector will have length 0 ]
transposeMat  {n = S m'}  xs = map head xs :: transposeMat (map tail xs)


dotP : (Num a) => {m : Nat} -> Vect m a -> Vect m a ->  a
dotP  xs ys = sum (zipWith (*) xs ys)


matMult : (Num a) => Vect m (Vect n a) -> Vect p (Vect n a) -> Vect m (Vect p a)
matMult {m = Z}  _  _ = []
matMult {m =  S m'} (x :: xs) ys = map (dotP x) ys :: matMult xs ys


matrixMult :  (Num a) => Vect m (Vect n a) -> Vect n (Vect p a) -> Vect m (Vect p a)
matrixMult xs ys = matMult xs (transposeMat ys)


matrixAdd : (Num a) => {m : Nat} -> {n : Nat} -> Vect m (Vect n a) -> Vect m (Vect n a) -> Vect m (Vect n a)
matrixAdd {m = Z} {n}  _ _ = []
matrixAdd {m = S m} {n} (x :: xs) (y :: ys) = zipWith (+) x y :: matrixAdd {m} {n} xs ys

*Matrix> matrixAdd [[1,2,3]] [[1,2,3]]
[[2, 4, 6]] : Vect 1 (Vect 3 Integer)
Metavariables: Main.addField

*Matrix> matrixAdd [[1,2,3]] [[1,2,3],[1,2,3]]
(input):1:22:When elaborating argument xs to constructor Data.VectType.Vect.:::
        Can't unify
                Vect (S n) a1 (Type of x :: xs)
        with
                Vect 0 (Vect 3 a) (Expected type)
        
        Specifically:
                Can't unify
                        S n
                with
                        0

For me using the dependent types in program is highly creative aspect and I still find this hard to use but it’s fun. Some resources which I have found very useful for learning. Idris [3], Coq [4], Dependent types at work [5], Type Theory Foundation [6] [7]. I am not expert in dependent type programming so if you have any suggestion/feedback then please drop your comment.

[1] http://en.wikipedia.org/wiki/Kind_%28type_theory%29
[2] http://lambda-the-ultimate.org/node/1129#comment-12313
[3] http://docs.idris-lang.org/en/latest/
[4] https://coq.inria.fr/
[5] http://www.cse.chalmers.se/~peterd/papers/DependentTypesAtWork.pdf
[6] https://www.youtube.com/watch?v=ev7AYsLljxk
[7] http://okmij.org/ftp/Haskell/dependent-types.html

List with concatenation operation is monoid.

We will try to prove in Coq that list with concatenation ( ++ ) is monoid. Monoid is set S with binary operation with following properties.
1). Closure.

2). Associativity.

3) Identity.

Proof in Coq.

Require Import List.

Theorem Closure : forall ( X : Type ) ( l1 l2 : list X ) , exists ( l3 : list X ),
   l1 ++ l2 = l3.
Proof.
 intros X l1 l2. exists ( l1 ++ l2) .
 reflexivity.
Qed.

Theorem Association : forall ( X : Type ) ( l1 l2 l3 : list X ) , 
  l1 ++ ( l2 ++ l3 ) = ( l1 ++  l2 ) ++ l3.
Proof.
  intros X l1 l2 l3.
  simpl. rewrite -> app_assoc_reverse. reflexivity.
Qed.

Theorem Existence_identity_left : forall ( X : Type ) ( l : list X ), exists e,
 e ++ l = l.
Proof.
 intros X l. exists nil. simpl.
 reflexivity.
Qed.

Theorem Existence_identify_right : forall ( X : Type ) ( l : list X ) , exists e,
  l ++ e = l.
Proof.
 intros X l. exists nil.
 apply app_nil_r.
Qed.

We don’t need to prove the closure property because all the functions in Coq is total. See thec discussion . Source code on github[1] and other proofs from software foundation[2].
[1] https://github.com/mukeshtiwari/Coq/blob/master/Monoid.v
[2] https://github.com/mukeshtiwari/Coq/blob/master/Poly.v

Proving Theorems in Coq

I recently started learning Coq from Software Foundations and I must say it’s highly addictive. Coq is theorem prover. When I started learning, the very first thing came to my mind is how is it possible for computer to prove theorem ?  In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems—and generally accepted statements, such as axioms[1]. From Coq’Art, Page 3 “The Coq system is not just another programming language. It actually makes it possible to express assertion about the values being manipulated. These value may range over mathematical objects or over programs”. Great so let me write a program and prove some properties using Coq.  The definition of Boolean and couple of functions over boolean

Inductive bool : Type :=
| true : bool
| false : bool.

Definition negb ( b : bool ) : bool :=
  match b with
  | true => false
  | false => true
  end.

Definition andb ( x : bool ) ( y : bool ) : bool :=
  match x with
  | true => y
  | false => false
  end.

Definition orb ( x : bool ) ( y : bool ) : bool :=
  match x with
  | false => y
  | true => true
  end.

Definition xorb ( x : bool ) ( y : bool ) : bool :=
  match x, y with
  | true, true => false
  | false, false => false
  | _, _  => true
  end.

Once we have some definitions, We can try to assert some properties about these functions. One assertion about XOR If output of xor is false it means both the inputs have same value. Lets write this theorem in Coq

Theorem xorb_equalleft : forall a b : bool, xorb a b = false -> a = b.

When Coq process this theorem, goal looks like this

1 subgoals, subgoal 1 (ID 97)
  
  ============================
   forall a b : bool, xorb a b = false -> a = b

and proof of the theorem is

Proof.
intros a b H. destruct a. destruct b.
reflexivity. discriminate.
destruct b. discriminate. reflexivity.
Qed.

Once the proof is complete, we will get the message from Coq “No more subgoals. xorb_equalleft is defined”. Lets define one more assertion about AND function. If the output of andb function is true it means both inputs are true.

Theorem andbc_true : forall b c : bool, andb b c = true -> b = true /\ c = true.

Coq proof of this assertion is

Proof.
intros b c. destruct b.
Case "b = true".
  simpl. intros H. split.
  reflexivity.
  rewrite <- H.
  reflexivity.
Case "b = false".
  simpl. intros H.
  discriminate.
Qed.

We have proved both the theorems but what is destruct, reflexivity, split and discriminate ? These are tactics and Coq is interactive theorem prover so you have to guide it towards goal using tactics. Source code on github[2]. Famous Theorems proved in Coq[3]. Certified Dependent type programming[4]

[1] http://en.wikipedia.org/wiki/Theorem
[2] https://github.com/mukeshtiwari/Coq
[3] http://perso.ens-lyon.fr/jeanmarie.madiot/coq100/
[4] http://adam.chlipala.net/cpdt/

yatra.com left my family stranded in midnight

You want to book a room in hotel which is fully occupied? No worries. Yatra can book a room for you in even fully occupied hotel. I booked a room in Hotel President in Patna Reference No. 28051438884, Hotel confirmation number: YAT0001458518 for one day from 31-05-2014 to 01-06-2014. Train arrived five hours late in Patna, my mother and sister some how managed to reach Hotel President at 1AM. Now the biggest part of booking plan that there was no booking! The hotel staff were surprised how come Yatra was able to book a room in completely occupied hotel. The staff of Hotel President did not let my family check in because there was no confirmation of booking/payment from Yatra to Hotel. I tried to call yatra.com at 1AM but there was no response because they work from 7AM-12AM. I tried to convince hotel staff but he simply replied that there is no vacant room so we can’t accommodate. I was really worried because they were complete stranger in the city, had no place to stay and next day my sister was going to appear in entrance examination. Some how I managed to call my friend and arranged the place for their stay but the question remains, how is it possible for company like Yatra to behave like this. After looking at their page on facebook, you can see in the review section that there is no happy customer and they don’t allow you to write on their wall. I found couple of links on mouthshut and counsumercourt about their service and customer satisfaction.
I am planning to file a case against yatra.com because it’s not business but fraud. If it’s possible for you then please share this post and spread the word.

Propositional Logic course ( Coursera )

Recently I took a logic course on Coursera. Although I am bit familiar with logic but this course was great. I got more clear grasp on Proposition logic, Proof tree, bit of Prolog and came to know about Quine–McCluskey algorithm ( in my TODO list of implementation ) while learning about circuit minimisation. In one of the assignments, we have to tell if the given formula is tautology, contradiction or contingent so I wrote some quick Haskell code to solve the assignment

import Text.Parsec.Prim
import Text.Parsec.Expr
import Text.Parsec.Char
import Text.Parsec.String ( Parser )
import Control.Applicative hiding ( ( <|> ) , many )
import qualified Data.Map as M
import Data.Maybe
import Data.List
import Control.Monad

data LExpr = Lit Char
           | Not LExpr       
           | And LExpr LExpr
           | Or LExpr LExpr
           | Imp LExpr LExpr  -- ( P =>  Q )
           | Red LExpr LExpr  -- ( P <=  Q )
           | Eqi LExpr LExpr  -- ( P <=> Q ) 
           deriving Show

exprCal :: Parser LExpr
exprCal = buildExpressionParser table atom 

table = [  [  Prefix ( Not <$ string  "~"  ) ]
         , [  Infix  ( And <$ string  "&"  ) AssocLeft ]
         , [  Infix  ( Or  <$ string  "|"  ) AssocLeft ]
         , [  Infix  ( Eqi <$ try ( string "<=>" ) ) AssocLeft 
            , Infix  ( Imp <$  string "=>"         ) AssocLeft 
            , Infix  ( Red <$  string "<="         ) AssocLeft 
           ]
        ]

atom :: Parser LExpr
atom =  char '(' *>  exprCal   <* char ')' 
     <|> ( Lit <$> letter )

assignment :: LExpr -> [ M.Map Char Bool ]
assignment expr = map ( M.fromList . zip vs ) ps where
    vs = variables expr
    ps = replicateM ( length vs ) [ True, False]
 

variables :: LExpr -> [ Char ]
variables expr = map head . group . sort . vars expr $ []  where
    vars ( Lit c )    xs = c : xs
    vars ( Not expr ) xs = vars expr xs
    vars ( And exprf exprs ) xs = vars exprf xs ++ vars exprs xs
    vars ( Or  exprf exprs ) xs = vars exprf xs ++ vars exprs xs
    vars ( Imp exprf exprs ) xs = vars exprf xs ++ vars exprs xs
    vars ( Red exprf exprs ) xs = vars exprf xs ++ vars exprs xs
    vars ( Eqi exprf exprs ) xs = vars exprf xs ++ vars exprs xs


expEval :: LExpr -> M.Map Char  Bool -> Bool
expEval ( Lit v   )         mp =  fromMaybe False ( M.lookup v mp )
expEval ( Not expr  )       mp =  not . expEval  expr $ mp
expEval ( And exprf exprs ) mp =  expEval exprf mp && expEval  exprs mp
expEval ( Or  exprf exprs ) mp =  expEval exprf mp || expEval  exprs mp
expEval ( Imp exprf exprs ) mp =  (  not . expEval  exprf $ mp  ) || expEval exprs mp 
expEval ( Red exprf exprs ) mp =  expEval ( Imp exprs exprf  ) mp 
expEval ( Eqi exprf exprs ) mp =  expEval exprf mp == expEval exprs mp

values :: LExpr -> [ Bool ]
values expr = map ( expEval expr ) ( assignment expr ) 

isTautology :: LExpr -> Bool
isTautology = and . values

isContradiction :: LExpr -> Bool
isContradiction  = not . or . values

isContingent :: LExpr -> Bool
isContingent expr = not ( isTautology expr || isContradiction expr )
  
calculator :: String -> LExpr
calculator expr = case parse  exprCal ""  expr of
                       Left msg -> error "failed to parse"
                       Right val -> val

Mukeshs-MacBook-Pro:Compilers mukeshtiwari$ ghci LogicPraser.hs 
GHCi, version 7.8.1: http://www.haskell.org/ghc/  😕 for help
Loading package ghc-prim ... linking ... done.
Loading package integer-gmp ... linking ... done.
Loading package base ... linking ... done.
[1 of 1] Compiling Main             ( LogicPraser.hs, interpreted )
Ok, modules loaded: Main.
*Main> calculator "p=>q|q=>p"
Loading package transformers-0.3.0.0 ... linking ... done.
Loading package array-0.5.0.0 ... linking ... done.
Loading package deepseq-1.3.0.2 ... linking ... done.
Loading package containers-0.5.5.1 ... linking ... done.
Loading package bytestring-0.10.4.0 ... linking ... done.
Loading package mtl-2.1.3.1 ... linking ... done.
Loading package text-1.1.1.1 ... linking ... done.
Loading package parsec-3.1.5 ... linking ... done.
Imp (Imp (Lit 'p') (Or (Lit 'q') (Lit 'q'))) (Lit 'p')
*Main> calculator "(p=>q)|(q=>p)"
Or (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p'))
*Main> isTautology ( Or (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p')) )
True
*Main> calculator "(p=>q)&(q=>p)"
And (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p'))
*Main> isTautology ( And (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p')) )
False
*Main> isCont ( And (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p')) )
isContingent     isContradiction
*Main> isContingent  ( And (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p')) )
True
*Main> isCont  ( And (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p')) )
isContingent     isContradiction
*Main> isContradiction   ( And (Imp (Lit 'p') (Lit 'q')) (Imp (Lit 'q') (Lit 'p')) )
False

Proof tree for propositional logic was something which I learned from this course. Why proof tree method is great ? We will take a example to understand it more clearly.

A set of premises Δ logically entails a conclusion ϕ (written as Δ |= ϕ) if and only if every interpretation that satisfies the premises also satisfies the conclusion. Logical formulas above the line are premises and below is conclusion.

We can see from the truth table that all the interpretation which satisfy premises also satisfy conclusion. Looks great but lengthy.
Proof tree rules

Theorem: Δ |= ϕ if and only if Δ ∪ {¬ϕ} is unsatisfiable. Following the theorem, our problem translates into proving that

is unsatisfiable. We can see that tree is closed and there is no interpretation which makes it satisfiable. Chose any branch and start moving up the tree and if it contains both A and ~A then we close the branch because it’s not possible to make A and ~A true simultaneously. You can see the course notes.
.
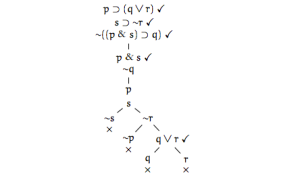See Propositional logic library from hackage. Source code on github

While Interpreter

Now a days I am trying to learn about static program analysis and started reading the Principal of Program Analysis. In order to understand the concepts, the book introduces a small programming language While.

I thought about writing interpreter for While to improve my Haskell skills. The very first task is in compilation/interpretation is breaking the source code into keywords, identifiers, operators, numbers and other tokens, known as lexical analysis. These tokens are passed to syntax analysis phase to combine the tokens into well formed expressions, statements and programs according to the grammar. The output of syntax analysis is abstract syntax tree which gives structural representation of of the input. Once we have abstract syntax tree, we can interpret or manipulate it for code generation. If you are interested in code generation then see Stephen Dielh blog.

The grammar for while program is

Grammar for expression
a  ::= x | n | - a | a opa a
b  ::= true | false | not b | b opb b | a opr a
opa ::= + | - | * | /
opb ::= and | or
opr ::= > | < 

Grammar for statements
S  ::= x := a | skip | S1; S2 | ( S ) | if b then S1 else S2 | while b do S 

The very first task is to define abstract syntax tree and Haskell algebraic data type makes this task almost trivial.

module AST ( Opa (..), Opb (..), Opr (..), AExpr (.. ) , BExpr ( .. ), 
             Stmt ( .. )  ) where



data Opa = Add
         | Sub
         | Mul
         | Div
         deriving Show

data Opb = And 
         | Or 
         deriving Show

data Opr = Greater 
         | Less 
         deriving Show


data AExpr = Var String
           | Num Integer
           | Neg AExpr
           | ABin Opa AExpr AExpr
           deriving Show

data BExpr = Con Bool
           | Not BExpr
           | BBin Opb BExpr BExpr
           | AL Opr AExpr AExpr
           deriving Show

data Stmt = List [ Stmt ]
          | Assing AExpr  AExpr
          | If BExpr Stmt Stmt
          | While BExpr Stmt
          | Skip
          deriving Show

The next task is design the lexical analyzer. We will use Parsec for this purpose.

module Lexer where
import Text.Parsec
import qualified Text.Parsec.Token as T
import Text.Parsec.Language ( emptyDef )
import Text.Parsec.String ( Parser )


lexer :: T.TokenParser ()
lexer = T.makeTokenParser emptyDef 
            {
                T.commentStart = "{-"
              , T.commentEnd = "-}"
              , T.reservedOpNames = [ "+", "-", "*", "/", ":=", ">", "<",
                                      "not", "and", "or" ]
              , T.reservedNames = [ "if", "then", "else", "while", "do", "skip",
                                  "true", "false" ]

            }


identifier :: Parser String
identifier = T.identifier lexer

whiteSpace :: Parser ()
whiteSpace = T.whiteSpace lexer

reserved :: String -> Parser ()
reserved = T.reserved lexer

reservedOp :: String -> Parser ()
reservedOp = T.reservedOp lexer

parens :: Parser a -> Parser a
parens = T.parens lexer

integer :: Parser Integer
integer = T.integer lexer

semi :: Parser String
semi =  T.semi lexer

semiSep :: Parser a -> Parser [ a ]
semiSep = T.semiSep lexer

Now lexical analyzer will assist the parser for creating the abstract syntax tree. A while program is list of statements and statement consists of expressions. We can build parse the expression by Parsec expression builder by giving the table of operators and associativity.

module Parser ( whileParser ) where

import Text.Parsec
import Text.Parsec.Expr
import Text.Parsec.String ( Parser )
import Control.Applicative  hiding ( (<|>) )
import Lexer
import AST

aTable = [  [   Prefix ( Neg <$ reservedOp "-" )                ]  
          , [   Infix  ( ABin Mul <$ reservedOp "*" ) AssocLeft
              , Infix  ( ABin Div <$ reservedOp "/" ) AssocLeft ]
          , [   Infix  ( ABin Add <$ reservedOp "+" ) AssocLeft
              , Infix  ( ABin Sub <$ reservedOp "-" ) AssocLeft ]
         ]



bTable = [  [  Prefix ( Not  <$ reservedOp "not" )               ]
          , [  Infix  ( BBin And <$ reservedOp "and" ) AssocLeft ] 
          , [  Infix  ( BBin Or  <$ reservedOp "or"  ) AssocLeft ]
         ] 
      
aExpression :: Parser AExpr
aExpression = buildExpressionParser aTable aTerm where 
         aTerm =  parens aExpression 
              <|> Var <$> identifier
              <|> Num <$> integer


bExpression :: Parser BExpr
bExpression = buildExpressionParser bTable bTerm where 
         bTerm =  parens bExpression 
              <|> (  Con True   <$ reserved "true"  ) 
              <|> (  Con False  <$ reserved "false" )
              <|> try (  AL Greater <$>  ( aExpression  <* reserved ">" ) 
                                    <*>    aExpression )
              <|> (  AL Less    <$>  ( aExpression  <* reserved "<" ) 
                                <*>    aExpression ) 


  

whileParser :: Parser Stmt
whileParser = whiteSpace *> stmtParser <* eof where 
            stmtParser :: Parser Stmt
            stmtParser =  parens stmtParser 
                      <|> List <$> sepBy stmtOne semi
            stmtOne :: Parser Stmt
            stmtOne =  ( Assing <$> ( Var <$> identifier ) 
                                <*> ( reserved ":=" *> aExpression ) )
                   <|> ( If <$> ( reserved "if" *> bExpression <* reserved "then" ) 
                            <*>   stmtParser 
                            <*> ( reserved "else" *> stmtParser ) )
                   <|> ( While <$> ( reserved "while" *> bExpression <*  reserved "do" ) 
                               <*>   stmtParser )
                   <|> ( Skip <$ reserved "nop" ) 

We have abstract syntax tree so we can interpret our program. You can think of a program as collection of commands which manipulates some memory location.

module Interpreter ( evalProgram )  where

import qualified Data.Map as M
import AST

type Store = M.Map String Integer

evalA :: AExpr -> Store -> Integer
evalA ( Var v ) s  =  M.findWithDefault 0 v s
evalA ( Num n ) _ = n
evalA ( Neg e ) s = - ( evalA e  s ) 
evalA ( ABin Add e1 e2 ) s = evalA e1 s + evalA e2 s
evalA ( ABin Sub e1 e2 ) s = evalA e1 s - evalA e2 s
evalA ( ABin Mul e1 e2 ) s = evalA e1 s * evalA e2 s
evalA ( ABin Div e1 e2 ) s = div ( evalA e1 s ) ( evalA e2 s )


evalB :: BExpr -> Store -> Bool
evalB ( Con b ) _ = b 
evalB ( Not e ) s = not ( evalB e s )
evalB ( BBin And e1 e2 ) s = ( && ) ( evalB e1 s )  ( evalB e2 s ) 
evalB ( BBin Or  e1 e2 ) s = ( || ) ( evalB e1 s )  ( evalB e2 s )
evalB ( AL Greater e1 e2 ) s = ( evalA e1 s ) > (  evalA e2 s )
evalB ( AL Less e1 e2 ) s = ( evalA e1 s ) < ( evalA e2 s )    

interpret :: Stmt -> Store -> Store
interpret ( Assing ( Var v ) expr ) s =  M.insert v ( evalA expr s )  s
interpret ( List [] ) s = s
interpret ( List ( x : xs ) ) s = interpret ( List xs ) ( interpret x s )
interpret ( If e st1 st2 ) s 
          | evalB e s = interpret st1 s
          | otherwise = interpret st2 s
interpret ( While e st ) s 
    | not t = s   
    | otherwise =  interpret ( While e st ) w 
    where
     t = evalB e s
     w = interpret st s

evalProgram :: Stmt -> Store
evalProgram st = interpret st M.empty

Now every thing is complete so let’s add main and write some while program.

module Main where
import System.Environment
import Text.Parsec
import Parser
import Interpreter




main = do 
     ( file : _ ) <- getArgs
     program <- readFile file
     case parse whileParser "" program of 
        Left e -> print e >> fail "Parse Error"
        Right ast -> print  ( evalProgram  ast )

While program to compute the greatest common divisor

Mukeshs-MacBook-Pro:whileinterpreter mukeshtiwari$ cat Gcd.while 
a := 10 ;
b := 100  ;
while ( b > 0 ) do 
 (
	t := b ;
    	b := a - ( a / b ) * b ;
	a := t 
)

Factorial program

Mukeshs-MacBook-Pro:whileinterpreter mukeshtiwari$ cat Fact.while 
x := 10 ;
y := x ;
z := 1 ;
while ( y > 1 )
  do 
   ( 
      z := z * y ;
      y := y - 1 
   );
y := 0 

Since our language doesn’t have IO instruction so we will have to see which variable store the result. In gcd program, the variable t stores the result and variable z stores the factorial of number.

Mukeshs-MacBook-Pro:src mukeshtiwari$ ghc -fforce-recomp Main.hs
[1 of 5] Compiling AST              ( AST.hs, AST.o )
[2 of 5] Compiling Lexer            ( Lexer.hs, Lexer.o )
[3 of 5] Compiling Interpreter      ( Interpreter.hs, Interpreter.o )
[4 of 5] Compiling Parser           ( Parser.hs, Parser.o )
[5 of 5] Compiling Main             ( Main.hs, Main.o )
Linking Main ...
Mukeshs-MacBook-Pro:src mukeshtiwari$ ./Main ../Gcd.while 
fromList [("a",10),("b",0),("t",10)]
Mukeshs-MacBook-Pro:src mukeshtiwari$ ./Main ../Fact.while 
fromList [("x",10),("y",0),("z",3628800)]

I am not expert in either Haskell or compiler so if you have any comments then please let me know. The complete source code on github.

2013 in review

The WordPress.com stats helper monkeys prepared a 2013 annual report for this blog.

Here’s an excerpt:

The concert hall at the Sydney Opera House holds 2,700 people. This blog was viewed about 18,000 times in 2013. If it were a concert at Sydney Opera House, it would take about 7 sold-out performances for that many people to see it.

Click here to see the complete report.

We, after 67 years of Independence

India has been invaded by many emperors since its inception but if we start looking back from colonial era, it is mainly ruled by British from 1757 – 1947. British ruled only here because of our nature to fight with each other[Battle of Plassey]. We were declared as free country on 15 August 1947 and from that day onwards we stand as one big nation. Did we learn anything from our mistakes in the past we committed. Probably not! Out of these 67 years, Indian National Congress is ruling the country for 48 of the 60 years since independence in 1947. Now below are some facts about how we are doing as a nation or we should be proud of

[1]Scams
We are very good at this and those who raised their voice against corruption is either killed or punished[ Satyendra Dubey and Ashok Khemka]. You haven’t seen enough! Our Minister of Home affairs Sushil Kumar Shinde on coal scam “Earlier, the Bofors was a talking point. People forgot about it. Now it is coal. This too will be forgotten. Once hands are washed off coal, they again become clean.” The union minister later said he was just joking. Certainly, this is joke on us that we elected you.

[2] Poverty
Our 33% population earns less than US$ 1.25 per day while 81 % live on less than US$ 2.50 per day[World Bank]. Quoting from The Guardian “A pledge to eliminate poverty has figured prominently in the election campaigns of all of India’s political parties since the country gained independence in 1947. Yet the ruling Congress party – and particularly prime minister Manmohan Singh, labelled as ‘Mr Silent’ for failing to answer questions on the landmark food security bill – is accused of exploiting poverty rather than putting in place effective measures to tackle it”.

[3] Literacy
The literacy rate in India stand to 74.04% in 2011 and the level is well below the world average literacy rate of 84%, and of all nations, India currently has the largest illiterate population. There are many reasons for this but I have a strong believe that lack of strong will power among political leaders to educate their people is the major reason.

[4] Communal violence
It’s very common among India to have a fight on very petty things. We are still fighting with each other for something happened 500 years ago[ RamJamanbhoomi ] and this led to many unfortunate events including Mumbai Bomb blast, Mumbai Riots and emergence of many terrorist groups. One of our leading political party BJP always promises to construct a temple to Rama at the site. They are still not aware that we have already payed a heavy price and lost many beloved ones!

Now why I am writing this ? Today a political party named Aam Aadmi Party formally launched on 26 November 2012 by Arvind Kejriwal defeated the Indian Nation Congress in Delhi elections. This is certainly not a miracle but because of their dedication to clean the Indian politics. Delhi is ruled by Indian Nation Congress for 15 years and Delhi holds the top position in crime against women. In 2012, We had seen the worst crime in Delhi[2012 Delhi gang rape]. Delhi government and Central government tried to downplay the crime but it was the protest of common man which pushed the government to act fast. It was the anger of common man against the corrupt politicians and promise of Arvind Kejriwal to clean the politics which swept away the Indian National Congress from Delhi. I hope Arvind Kejriwal would fulfill his promise to clean the politics and I will remember this day ( 8 December 2013 ) as a day in history which changed the India and Indian Politics.

Proving the correctness of code using SMT sovler.

SMT solvers are great tool in computer science. One use of these solvers to prove the correctness of code. I wrote Haskell code to compute the inverse of polynomial using extended euclidean algorithm in Galois Field GF ( 2ⁿ ). If we try to analyze the code of inversePolynomial then every thing is normal except passing the depth parameter. It is unnecessary because we know that recursion is going to terminate. Initially I wrote the code without depth and the program was not terminating so I wrote mail to Levent Erkok and according to him

Your code suffers from what’s known as the “symbolic termination”. See Section 7.4 of: http://goo.gl/0E7wkm for a discussion of this issue in the context of Cryptol; but the same comments apply here as well. Briefly, when you recurse in inversePoly, SBV does not know when to stop the recursion of both branches in the ite: Thus it keeps expanding both branches ad infinitum.

Luckily, symbolic termination is usually easy to deal with once you identify what the problem is. Typically, one needs to introduce a recursion depth counter, which would stop recursion when it reaches a pre-determined depth that is determined to be safe. In fact, SBV comes with the regular GCD example that talks about this issue in detail:

http://hackage.haskell.org/packages/archive/sbv/2.10/doc/html/Data-SBV-Examples-CodeGeneration-GCD.html

I’d recommend reading the source code of the above; it should clarify the problem. You’ll need to find out a recursion-depth that’ll work for your example (try running it on concrete values and coming up with a safe number); and then prove that the bound is actually correct as explained in the above. The recursion depth bound just needs to be an overapproximation: If the algorithm needs 20 iterations but you use 30 as your recursion depth, nothing will go wrong; it’ll just produce bigger code and thus be less efficient and maybe more complicated for the backend prover. Of course, if you put a depth of 18 when 20 is needed, then it will be wrong and you won’t be able to establish correctness.

My verification condition is inverse of inverse of polynomial is same as polynomial. Right now I have no idea about proving the upper bound on depth so I just took 20. If you have any suggestion/comments then please let me know.

import Data.SBV.Bridge.Z3
import Data.Maybe


inversePolynomial ::  [ Int ] -> [ Int ] ->  SWord16
inversePolynomial poly reducer =  inversePoly  reducer' rem' first' second' depth'  where
                        poly' =  polynomial poly :: SWord16
                        reducer' =  polynomial reducer :: SWord16
                        first' =  0 :: SWord16
                        second' = 1 :: SWord16
                        depth' = 20 :: SWord16
                        ( quot', rem' ) = pDivMod poly' reducer'

inversePoly :: SWord16 -> SWord16 -> SWord16 -> SWord16  ->  SWord16 -> SWord16
inversePoly  reducer'' poly'' first'' second'' depth'' =
               ite ( depth'' .== 0 ||| rem'' .== ( 0 :: SWord16 ) ) (  second'' )  ( inversePoly  poly'' rem'' second'' ret ( depth'' - 1 ) )  where
                                   ( quot'', rem'' ) = pDivMod reducer'' poly''
                                   ret =  pAdd ( pMult ( quot'', second'', [] ) ) first''

isInversePolyCorrect :: SWord16 -> SWord16 -> SBool
isInversePolyCorrect poly reducer = inversePoly reducer ( inversePoly reducer rem first second depth ) first second depth .== rem where
                        ( quot, rem ) = pDivMod  poly reducer
                        first = 0 :: SWord16
                        second = 1 :: SWord16
                        depth = 20 :: SWord16

*Main> showPoly ( inversePolynomial  [ 6,4,1,0] [ 8,4,3,1,0] )
"x^7 + x^6 + x^3 + x"
*Main> proveWith z3 { verbose=False }  $ forAll ["x"] $ \x ->  pMod x ( 283 :: SWord16 ) ./=0 ==> isInversePolyCorrect x ( 283 :: SWord16 ) 
Q.E.D.
*Main> proveWith cvc4 { verbose=False }  $ forAll ["x"] $ \x ->  pMod x ( 283 :: SWord16 ) ./=0 ==> isInversePolyCorrect x ( 283 :: SWord16 ) 
*** Exception: fd:10: hFlush: resource vanished (Broken pipe)
*Main> proveWith yices { verbose=False }  $ forAll ["x"] $ \x ->  pMod x ( 283 :: SWord16 ) ./=0 ==> isInversePolyCorrect x ( 283 :: SWord16 ) 
Q.E.D.